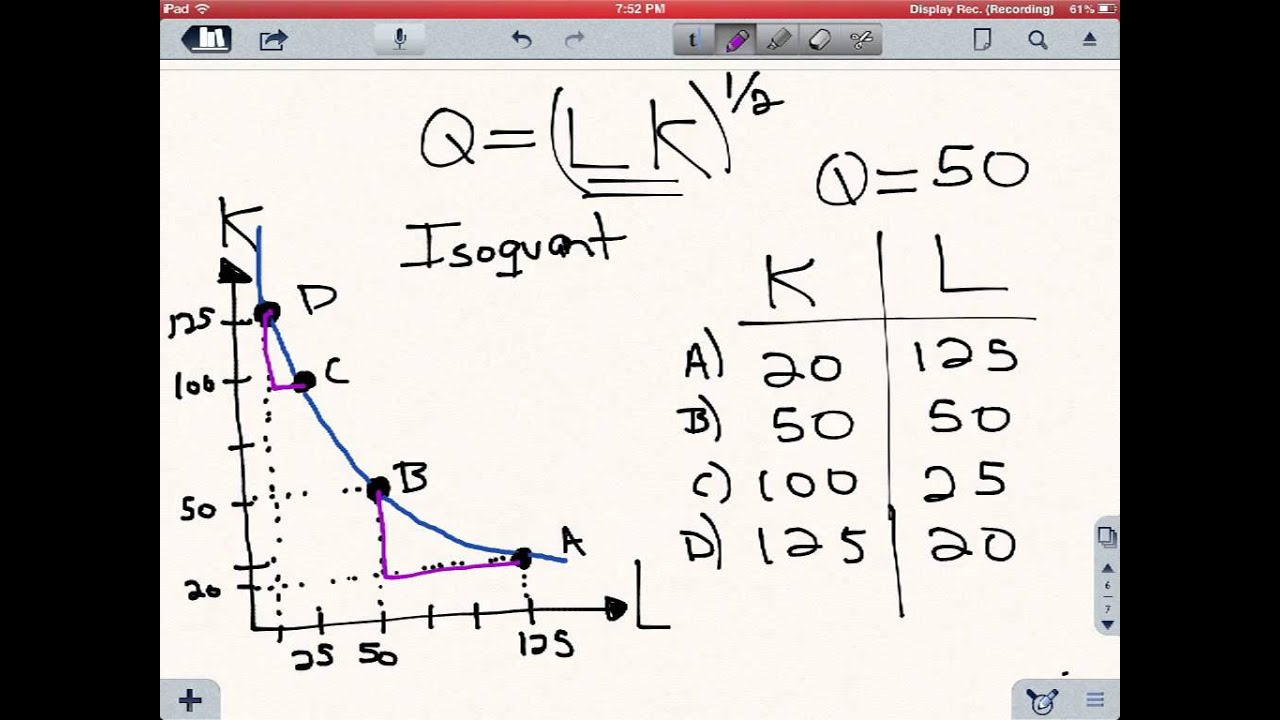
Given a production function for a certain output, one can derive isoquant showing all the combinations of the factors of production that yield the same level of output. This is done by substituting the value of output in the production function and by getting different values of one factor for different values of another factor.
Isoquants or equal-product or iso-product curves are analogous to the indifference curves of the consumer theory. An isoquant is one of the ways of presenting production, where the two factors of production are explicitly shown. It represents all possible input combinations (input ratios) of the two factors, which are capable of producing the same level of output. Thus, input ratio keeps on changing along an isoquant.
As producer would be indifferent between such combinations, so it is often referred to as the producer’s indifference curve or production indifference curve. All combinations yielding the same level of output lie on the same iso-product curve or production indifference curve. It is a contour line showing the points of equal production on a map showing production as its dimensions.
ADVERTISEMENTS:
In the words of Keirstead, “Iso-product curve represents all possible combinations of the two factors that will give the same total product”. According to K.J. Cohen and R.M. Cyert, “An iso-product curve is a curve along which the maximum achievable production is constant”.
Iso-product curve analysis helps a producer to find a combination of two factors, which gives him maximum output at the minimum cost. In other words, this analysis solves the problem of optimum combination of factors.
Various factor combinations ‘A’, ‘B’, ‘C’, ‘D’ and ‘E’ producing the same level of output, say 100 units are shown in the following Fig. 7.2 in the form of isoquant IQ. These points depict different techniques of production.
ADVERTISEMENTS:
For example, point ‘A’ represents capital intensive technique, while point ‘E’ represents labour intensive technique. Technology is assumed to remain unchanged and inputs are assumed to be perfectly divisible.
In isoquant IQ shown in Fig. 7.2, as the quantity of one factor is reduced, the quantity of other factor will have to be increased, so that the total product remains the same. A number of isoquants (i.e., family of isoquants) depicting different amounts of output are known as isoquant map.
It represents technical conditions of production for a product. Input ratios may remain constant on various points of different isoquants, where a ray from origin cuts them. Fig. 7.2 shows such an isoquant map, where isoquant IQ represents the lowest output level of 100 units, while isoquants IQ1, IQ2 and IQ3 represent higher output levels of 200 units, 300 units and 400 units respectively.
ADVERTISEMENTS:
It must be noted that each higher isoquant shows higher output than the lower one, because, every point on such curve implies greater amount of at least one factor than some point on the lower isoquant one, while every individual isoquant shows the same level of output.
Various levels of output may be producible by the same input ratio, while the input ratio may change for a given level of output. This family of isoquants represents a production function with two variable inputs.